Introduction

1. Introduction

2. Why Study Data Structures and Abstract Data Types?

3. Getting Started with Data

4. Review of Programming

5. Review of OOP

1.1~1.4 Introduction

Given a problem, a computer scientist’s goal is to develop an algorithm, a step-by-step list of instructions for solving any instance of the problem that might arise. Algorithms are finite processes that if followed will solve the problem.

source: https://www.owkin.com/a-z-of-ai-for-healthcare/algorithm

It is very common to include the word computable when describing problems and solutions. We say that a problem is computable if an algorithm exists for solving it. A definition for computer science is to study the problems that are and that are not computable!

Computer science is also the study of abstraction. Abstraction allows us to view the problem and solution in such a way as to separate the so-called logical and physical perspectives.

For instance, you are using the functions provided by the vehicle designers for the purpose of transporting you from one location to another. These functions are sometimes also referred to as the interface.

As another example of abstraction, consider the Python math module. Once we import the module, we can perform computations such as

import math

math.sqrt(16)

4.0

This is an example of procedural abstraction.

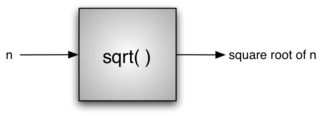
Programming is the process of encoding an algorithm into a programming language, so that it can be executed by a computer. Programming languages must provide ways to represent both the process and the data which is known as control constructs and data types.

Control constructs allow algorithmic steps to be represented in a convenient yet unambiguous way.

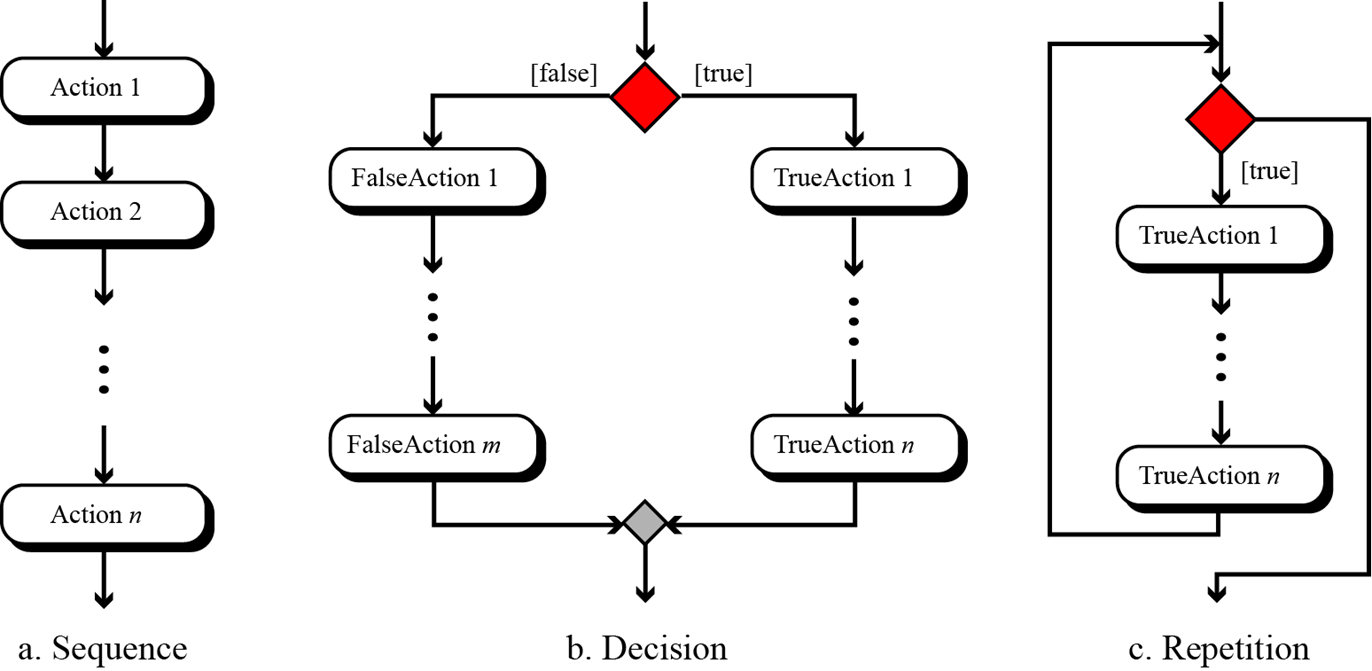
We give the formal definition of algorithm here:

1. Well-Defined: An algorithm must be a well-defined, ordered set of instructions.

2. Unambiguous steps: If one step is to add two integers, we must define both ‘integers’ as well as the ‘add’ operation

3. Produce a result: An algorithm must produce a result. The result can be data returned or some other effect (for example, printing).

4. Terminate in a finite time: An algorithm must terminate. If it does not, we have not created an algorithm!

1.5 Why Study Data Structures and Abstract Data Types?

The data abstraction share a similar idea with procedure abstraction. An abstract data type, sometimes abbreviated ADT, is a logical description of how we view the data and the operations that are allowed without regard to how they will be implemented.

By providing this level of abstraction, we are creating an encapsulation around the data. The idea is that by encapsulating the details of the implementation, we are hiding them from the user's view.

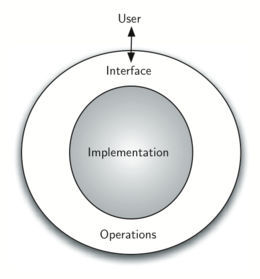
The implementation of an abstract data type, often referred to as a data structure, will require that we provide a physical view of the data using some collection of programming constructs and primitive data types.

The separation of these two perspectives will allow us to provide an implementation-independent view of the data.

There will usually be many different ways to implement an abstract data type and the user can remain focused on the problem-solving process.

1.6 Why Study Algorithms?

Being exposed to different problem-solving techniques and seeing how different algorithms are designed to help us. We can then begin to develop pattern recognition so that the next time a similar problem arises, we are better able to solve it!

On the other hand, it is entirely possible that there are many different ways to implement the details to algorithm. One algorithm may use many fewer resources than another. We would like to have some way to compare these solutions. Even though they both work, one is perhaps "better" than the other.

As we study algorithms, we can learn analysis techniques that allow us to compare and contrast solutions based solely on their own characteristics, not the characteristics of the program or computer used to implement them.

There will often be trade-offs that we will need to identify and decide upon. As computer scientists, in addition to our ability to solve problems, we will also need to know and understand solution evaluation techniques.

1.8 Getting Started with Data

In Python, as well as in any other object-oriented programming language, we define a class to be a description of what the data look like (the state) and what the data can do (the behavior).

Classes are analogous to abstract data types because a user of a class only sees the state and behavior of an objects in the object-oriented paradigm. An object is an instance of a class.

1.8.1 Built-in Atomic Data Types

Python has two main built-in numeric classes that implement the integer and floating-point data types. These Python classes are called int and float. The standard arithmetic operators, +, -, *, /, % (modulo), // (integer division) and ** (exponentiation), can be used:

print(2 + 3 * 4)
print((2 + 3) * 4)
print(2 ** 10)
print(6 / 3)
print(7 / 3)
print(7 // 3)
print(7 % 3)
print(2 ** 100)

14
20
1024
2.0
2.3333333333333335
2
1
1267650600228229401496703205376

The Boolean data type, implemented as the Python bool class, will be quite useful for representing truth values. The possible state values for a Boolean object are True and False with the standard Boolean operators, and, or, and not.

print(False or True)
print(not (False or True))
print(True and True)

True
False
True

Boolean data objects are also used as results for comparison operators such as equality (==) and greater than (>). The table below shows the relational and logical operators.

Operation Name	Operator	Explanation
less than	<	Less than operator
greater than	>	Greater than operator
less than or equal	<=	Less than or equal to operator
greater than or equal	>=	Greater than or equal to operator
equal	==	Equality operator
not equal	!=	Not equal operator
logical and	and	Both operands True for result to be True
logical or	or	One or the other operand is True for the result to be True
logical not	not	Negates the truth value, False becomes True, True becomes False

print(5 == 10)
print(10 > 5)
print((5 >= 1) and (5 <= 10))
print((1 < 5) or (10 < 1))
print(1 < 5 < 10)

False
True
True
True
True

Identifiers are used in programming languages as names. In Python, identifiers start with a letter or an underscore (_), are case sensitive, and can be of any length.

A Python variable is created when a name is used for the first time on the left-hand side of an assignment statement. Assignment statements provide a way to associate a name with a value. The variable will hold a reference to a piece of data but not the data itself.

the_sum = 0
print(the_sum)

the_sum = the_sum + 1
print(the_sum)

the_sum = True
print(the_sum)

0
1
True

The assignment statement the_sum = 0 creates a variable and lets it hold the reference to the data object 0.

At this point in our example, the type of the variable is integer as that is the type of the data currently being referred to by the_sum.

If the type of the data changes, as shown above with the Boolean value True, so does the type of the variable (the_sum is now of the type Boolean).

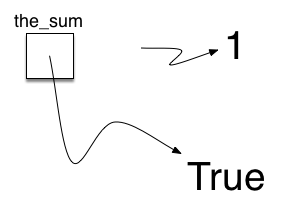
The assignment statement changes the reference being held by the variable. This is a dynamic characteristic of Python. The same variable can refer to many different types of data.

1.8.2. Built-in Collection Data Types

Python has a number of very powerful built-in collection classes. Lists, strings, and tuples are ordered collections (sequence) that are very similar in general structure. Sets and dictionaries are unordered collections.

A list is an ordered collection of zero or more references to Python data objects. Lists are heterogeneous, meaning that the data objects need not all be from the same class and the collection can be assigned to a variable as below.

my_list = [1, 3, True, 6.5]
my_list

[1, 3, True, 6.5]

Since lists are considered to be sequentially ordered, they support a number of operations that can be applied to any Python sequence.

Operation Name	Operator	Explanation
indexing	[ ]	Access an element of a sequence
concatenation	+	Combine sequences together
repetition	*	Concatenate a repeated number of times
membership	in	Ask whether an item is in a sequence
length	len	Ask the number of items in the sequence
slicing	[ : ]	Extract a part of a sequence

Note that the indices for lists start counting with 0. The slice operation my_list[1:3] returns a list of items starting with the item indexed by 1 up to—but not including—the item indexed by 3.

Lists support a number of methods that will be used to build data structures.

Method Name	Use	Explanation
append	a_list.append(item)	Adds a new item to the end of a list
insert	a_list.insert(i,item)	Inserts an item at the ith position in a list
pop	a_list.pop()	Removes and returns the last item in a list
pop	a_list.pop(i)	Removes and returns the ith item in a list
sort	a_list.sort()	Sorts a list in place
reverse	a_list.reverse()	Modifies a list to be in reverse order
del	del a_list[i]	Deletes the item in the ith position
index	a_list.index(item)	Returns the index of the first occurrence of item
count	a_list.count(item)	Returns the number of occurrences of item
remove	a_list.remove(item)	Removes the first occurrence of item

my_list = [1024, 3, True, 6.5]
my_list.append(False)
print(my_list)
my_list.insert(2,4.5)
print(my_list)
print(my_list.pop())
print(my_list)
print(my_list.pop(1))
print(my_list)
my_list.pop(2)
print(my_list)

[1024, 3, True, 6.5, False]
[1024, 3, 4.5, True, 6.5, False]
False
[1024, 3, 4.5, True, 6.5]
3
[1024, 4.5, True, 6.5]
[1024, 4.5, 6.5]

my_list.sort()
print(my_list)
my_list.reverse()
print(my_list)
print(my_list.count(6.5))
print(my_list.index(4.5))
my_list.remove(6.5)
print(my_list)
del my_list[0]
print(my_list)

[4.5, 6.5, 1024]
[1024, 6.5, 4.5]
1
2
[1024, 4.5]
[4.5]

You can see that some of the methods, such as pop(), return a value and also modify the list. Others, such as reverse(), simply modify the list with no return value. You should also notice the familiar "dot" notation for asking an object to invoke a method.

In fact, even simple data objects such as integers can invoke methods in this way.

(54).__add__(21) # Equal to 54+21

75

One common Python function that is often discussed in conjunction with lists is the range() function. range() produces a range object that represents a sequence of values.

print(range(10))
print(list(range(10)))
print(range(5, 10))
print(list(range(5, 10)))
print(list(range(5, 10, 2)))
print(list(range(10, 1, -1)))

range(0, 10)
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
range(5, 10)
[5, 6, 7, 8, 9]
[5, 7, 9]
[10, 9, 8, 7, 6, 5, 4, 3, 2]

Strings are sequential collections of zero or more letters, numbers, and other symbols. Literal string values are differentiated from identifiers by using quotation marks (either single or double):

print("David")
print('David')
my_name = "David"
print(my_name[3])
print(my_name * 2)
print(len(my_name))

David
David
i
DavidDavid
5

A major difference between lists and strings is that lists can be modified while strings cannot. This is referred to as mutability. Lists are mutable; strings are immutable.

print(my_list)
my_list[0] = 2 ** 10
print(my_list)

print(my_name)
my_name[0] = "X"

[4.5]
[1024]
David

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
~\AppData\Local\Temp\ipykernel_19312\1799471016.py in <module>
      4 
      5 print(my_name)
----> 6 my_name[0] = "X"

TypeError: 'str' object does not support item assignment

Tuples are very similar to lists in that they are heterogeneous sequences of data. The difference is that a tuple is immutable, like a string. As sequences, they can use operation described above:

my_tuple = (2, True, 4.96)
print(my_tuple)
print(len(my_tuple))
print(my_tuple[0])
print(my_tuple * 3)
print(my_tuple[0:2])

my_tuple[1] = False

(2, True, 4.96)
3
2
(2, True, 4.96, 2, True, 4.96, 2, True, 4.96)
(2, True)

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
~\AppData\Local\Temp\ipykernel_19312\329028039.py in <module>
      6 print(my_tuple[0:2])
      7 
----> 8 my_tuple[1] = False

TypeError: 'tuple' object does not support item assignment

A set is an unordered collection of zero or more immutable Python data objects. Sets do not allow duplicates. The empty set is represented by set():

my_set = {3, 6, "cat", 4.5, False}
my_set

{3, 4.5, 6, False, 'cat'}

Even though sets are not considered to be sequential, they do support a few of the familiar operations presented earlier.

Operation Name	Operator	Explanation
membership	in	Set membership
length	len	Returns the cardinality of the set
union	a_set \| other_set	Returns a new set with all elements from both sets
intersection	a_set & other_set	Returns a new set with only those elements common to both sets
difference	a_set - other_set	Returns a new set with all items from the first set not in the second
subset	a_set <= other_set	Asks whether all elements of the first set are in the second

print(len(my_set))
print(False in my_set)
print("dog" in my_set)

5
True
False

Our final Python collection is an unordered structure called a dictionary. Dictionaries are collections of associated pairs of items where each pair consists of a key and a value. This key-value pair is typically written as key:value.

capitals = {"Iowa": "Des Moines", "Wisconsin": "Madison"}
capitals

{'Iowa': 'Des Moines', 'Wisconsin': 'Madison'}

We can manipulate a dictionary by accessing a value via its key or by adding another key-value pair. The syntax for access looks much like a sequence access except that instead of using the index of the item, we use the key value.

capitals = {"Iowa": "Des Moines", "Wisconsin": "Madison"}
print(capitals["Iowa"])
capitals["Utah"] = "Salt Lake City"
print(capitals)
capitals["California"] = "Sacramento"
print(len(capitals))
for k in capitals:
    print(capitals[k],"is the capital of", k)

Des Moines
{'Iowa': 'Des Moines', 'Wisconsin': 'Madison', 'Utah': 'Salt Lake City'}
4
Des Moines is the capital of Iowa
Madison is the capital of Wisconsin
Salt Lake City is the capital of Utah
Sacramento is the capital of California

Dictionaries have both methods and operators. The keys(), values(), and items() methods all return objects that contain the values of interest.

Operator	Use	Explanation
[]	a_dict[k]	Returns the value associated with k, otherwise its an error
in	key in a_dict	Returns True if key is in the dictionary, False otherwise
del	del a_dict[key]	Removes the entry from the dictionary

Method Name	Use	Explanation
keys	a_dict.keys()	Returns the keys of the dictionary in a dict_keys object
values	a_dict.values()	Returns the values of the dictionary in a dict_values object
items	a_dict.items()	Returns the key-value pairs in a dict_items object
get	a_dict.get(k)	Returns the value associated with k, None otherwise
get	a_dict.get(k, alt)	Returns the value associated with k, alt otherwise

phone_ext={"david": 1410, "brad": 1137, "roman": 1171}
print(phone_ext)
print(phone_ext.keys())
print(list(phone_ext.keys()))
print(phone_ext.values())
print(list(phone_ext.values()))
print(phone_ext.items())
print(list(phone_ext.items()))
print(phone_ext.get("kent"))
print(phone_ext.get("kent", "NO ENTRY"))

{'david': 1410, 'brad': 1137, 'roman': 1171}
dict_keys(['david', 'brad', 'roman'])
['david', 'brad', 'roman']
dict_values([1410, 1137, 1171])
[1410, 1137, 1171]
dict_items([('david', 1410), ('brad', 1137), ('roman', 1171)])
[('david', 1410), ('brad', 1137), ('roman', 1171)]
None
NO ENTRY

1.9. Input and Output

Python provides us with a function that allows us to ask a user to enter some data and returns a reference to the data in the form of a string. The function is called input.

Python’s function input takes a single parameter that is a string. This string is often called the prompt because it contains some helpful text prompting the user to enter something

a_name = input("Please enter your name: ")
print("Your name in all capitals is", a_name.upper(),
      "and has length", len(a_name))

Please enter your name: phonchi
Your name in all capitals is PHONCHI and has length 7

It is important to note that the value returned from the input function will be a string representing the exact characters that were entered after the prompt. If you want this string interpreted as another type, you must provide the type conversion explicitly.

s_radius = input("Please enter the radius of the circle ")
print(s_radius)
radius = float(s_radius)
print(radius)
diameter = 2 * radius
print(diameter)

Please enter the radius of the circle 3
3
3.0
6.0

1.9.1. String Formatting

print() takes zero or more parameters and displays them using a single blank as the default separator. It is possible to change the separator character by setting the sep argument. In addition, each print ends with a newline character by default. This behavior can be changed by setting the end argument.

print("Hello")
print("Hello", "World")
print("Hello", "World", sep="***")
print("Hello", "World", end="***")
print("Hello")

Hello
Hello World
Hello***World
Hello World***Hello

It is often useful to have more control over the look of your output. Fortunately, Python provides us with an alternative called formatted strings. A formatted string is a template in which words or spaces that will remain constant are combined with placeholders for variables that will be inserted into the string.

age = 20
print(a_name, "is", age, "years old.")
print("%s is %d years old." % (a_name, age))

phonchi is 20 years old.
phonchi is 20 years old.

The % operator is a string operator called the format operator. The left side of the expression holds the template or format string, and the right side holds a collection of values that will be substituted into the format string.

The format string may contain one or more conversion specifications. A conversion character tells the format operator what type of value is going to be inserted into that position in the string. In the example above, the %s specifies a string, while the %d specifies an integer.

Character	Output Format
d, i	Integer
u	Unsigned integer
f	Floating point as m.ddddd
e	Floating point as m.ddddde+/-xx
E	Floating point as m.dddddE+/-xx
g	Use %e for exponents less than -4 or greater than +5, otherwise use %f
c	Single character
s	String, or any Python data object that can be converted to a string by using the str function
%	Insert a literal % character

Python 3.6 introduced f-strings, a way to use proper variable names instead of placeholders. Formatting conversion symbols can still be used inside an f-string, but the alignment symbols are different from those used with placeholders

Modifier	Example	Description
number	:20d	Put the value in a field width of 20
<	:<20d	Put the value in a field 20 characters wide, left-aligned
>	:>20d	Put the value in a field 20 characters wide, right-aligned
^	:^20d	Put the value in a field 20 characters wide, center-aligned
0	:020d	Put the value in a field 20 characters wide, fill in with leading zeros
.	:20.2f	Put the value in a field 20 characters wide with 2 characters to the right of the decimal point

price = 24
item = "banana"
print(f"The {item:10} costs {price:10.2f} cents")
print(f"The {item:<10} costs {price:<10.2f} cents")
print(f"The {item:^10} costs {price:^10.2f} cents")
print(f"The {item:>10} costs {price:>10.2f} cents")
print(f"The {item:>10} costs {price:>010.2f} cents")
itemdict = {"item": "banana", "price": 24}
print(f"Item:{itemdict['item']:.>10}\n" +
    f"Price:{'$':.>4}{itemdict['price']:5.2f}")

The banana     costs      24.00 cents
The banana     costs 24.00      cents
The   banana   costs   24.00    cents
The     banana costs      24.00 cents
The     banana costs 0000024.00 cents
Item:....banana
Price:...$24.00

1.10. Control Structures

As we noted earlier, algorithms require two important control structures: iteration and selection. Both of these are supported by Python in various forms. For iteration, Python provides a standard while statement and a very powerful for statement. The while statement repeats a body of code as long as a condition evaluates to True:

counter = 1
while counter <= 5:
    print("Hello, world")
    counter = counter + 1

Hello, world
Hello, world
Hello, world
Hello, world
Hello, world

It is easy to see the structure of a Python while statement due to the mandatory indentation pattern that the language enforces.

Even though this type of construct is very useful in a wide variety of situations, another iterative structure, the for statement, can be used in conjunction with many of the Python collections. The for statement can be used to iterate over the members of a collection, so long as the collection is a sequence.

for item in [1, 3, 6, 2, 5]:
    print(item)

1
3
6
2
5

A common use of the for statement is to implement definite iteration over a range of values.

for item in range(5):
    print(item ** 2)

0
1
4
9
16

Selection statements allow programmers to ask questions and then, based on the result, perform different actions. Most programming languages provide two versions of this useful construct: the if...else and the if. A simple example of a binary selection uses the if...else statement.

import math
n = 16
if n < 0:
    print("Sorry, value is negative")
else:
    print(math.sqrt(n))

4.0

Selection constructs, as with any control construct, can be nested so that the result of one question helps decide whether to ask the next. For example, assume that score is a variable holding a reference to a score for a computer science test.

score = 85
if score >= 90:
    print("A")
else:
    if score >= 80:
        print("B")
    else:
        if score >= 70:
            print("C")
        else:
            if score >= 60:
                print("D")
            else:
                print("F")

B

An alternative syntax for this type of nested selection uses the elif keyword. Note that the final else is still necessary to provide the default case if all other conditions fail.

if score >= 90:
    print("A")
elif score >= 80:
    print("B")
elif score >= 70:
    print("C")
elif score >= 60:
    print("D")
else:
    print("F")

B

Returning to lists, there is an alternative method for creating a list that uses iteration and selection constructs known as a list comprehension. A list comprehension allows you to easily create a list based on some processing or selection criteria.

sq_list = []
for x in range(1, 11):
    sq_list.append(x * x)

print(sq_list)

sq_list=[x * x for x in range(1, 11)]
sq_list

[1, 4, 9, 16, 25, 36, 49, 64, 81, 100]

[1, 4, 9, 16, 25, 36, 49, 64, 81, 100]

The general syntax for a list comprehension also allows a selection criteria to be added so that only certain items get added.

sq_list=[x * x for x in range(1,11) if x % 2 != 0]
sq_list

[1, 9, 25, 49, 81]

Exercise: Develop a function average that takes a list of integers, aList, calculates their average, and prints "pass" or "fail" based on the average being >=60 or not, respectively. Include the average score rounded to one decimal place in the output.

def average(aList):
    #Your code here

average([99, 100, 74, 63, 100, 100])
average([22, 19, 74, 63, 100, 44])

pass, the score is 89.3
fail, the score is 53.7

1.11. Exception Handling

There are two types of errors that typically occur when writing programs. The first, known as a syntax error, simply means that the programmer has made a mistake in the structure of a statement or expression.

for i in range(10)

  File "C:\Users\adm\AppData\Local\Temp\ipykernel_19312\1522442676.py", line 1
    for i in range(10)
                      ^
SyntaxError: invalid syntax

The other type of error, known as a logic error, denotes a situation where the program executes but gives the wrong result. This can be due to an error in the underlying algorithm or an error in your translation of that algorithm.

In some cases, logic errors lead to very bad situations such as trying to divide by zero or trying to access an item in a list where the index of the item is outside the bounds of the list. In this case, the logic error leads to a runtime error that causes the program to terminate! These types of runtime errors are typically called exceptions.

Most programming languages provide a way to deal with these errors that will allow the programmer to have some type of intervention if they so choose. In addition, programmers can create their own exceptions if they detect a situation in the program execution that warrants it.

When an exception occurs, we say that it has been raised. You can handle the exception that has been raised by using a try statement.

import math
a_number = int(input("Please enter an integer "))
print(math.sqrt(a_number))

Please enter an integer -3

---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
~\AppData\Local\Temp\ipykernel_19312\131839230.py in <module>
      1 import math
      2 a_number = int(input("Please enter an integer "))
----> 3 print(math.sqrt(a_number))

ValueError: math domain error

We can handle this exception by calling the print function from within a try block. A corresponding except block "catches" the exception and prints a message back to the user in the event that an exception occurs.

try:
    a_number = int(input("Please enter an integer "))
    print(math.sqrt(a_number))
except:
    print("Bad value for the square root function")
    print("Using the absolute value instead")
    print(math.sqrt(abs(a_number)))

Please enter an integer -3
Bad value for the square root function
Using the absolute value instead
1.7320508075688772

It is also possible for a programmer to cause a runtime exception by using the raise statement. For example, instead of calling the square root function with a negative number, we could have checked the value first and then raised our own exception!

if a_number < 0:
    raise RuntimeError("You can't use a negative number")
else:
    print(math.sqrt(a_number))

---------------------------------------------------------------------------
RuntimeError                              Traceback (most recent call last)
~\AppData\Local\Temp\ipykernel_19312\1609119426.py in <module>
      1 if a_number < 0:
----> 2     raise RuntimeError("You can't use a negative number")
      3 else:
      4     print(math.sqrt(a_number))

RuntimeError: You can't use a negative number

1.12. Defining Functions

The earlier example of procedural abstraction called upon a Python function called sqrt() from the math module to compute the square root. In general, we can hide the details of any computation by defining a function. A function definition requires a name, a group of parameters, and a body. It may also explicitly return a value.

def square(n):
     return n ** 2

print(square(3))

square(square(3))

9

81

1.13. Object-Oriented Programming in Python: Defining Classes

One of the most powerful features in an object-oriented programming language is the ability to allow a programmer (problem solver) to create new classes that model data that is needed to solve the problem.

Remember that we use abstract data types to provide the logical description of what a data object looks like (its state) and what it can do (its methods).

1.13.1. A Fraction Class

A very common example to show the details of implementing a user-defined class is to construct a class to implement the abstract data type Fraction. Although it is possible to create a floating point approximation for any fraction, in this case we would like to represent the fraction as an exact value.

The operations for the Fraction type will allow a Fraction data object to behave like any other numeric value. We need to be able to add, subtract, multiply, and divide fractions.

We also want to be able to show fractions using the standard "slash" form, for example 3/5. In addition, all fraction methods should return results in their lowest terms so that no matter what computation is performed, we always end up with the most common form.

In Python, we define a new class by providing a name and a set of method definitions that are syntactically similar to function definitions. The first method that all classes should provide is the constructor. The constructor defines the way in which data objects are created.

class Fraction:
    """Class Fraction"""
    def __init__(self, top, bottom):
        """Constructor definition"""
        self.num = top
        self.den = bottom

self is a special parameter that will always be used as a reference back to the object itself. It must always be the first formal parameter.

To create an instance of the Fraction class, we must invoke the constructor.

my_fraction = Fraction(3, 5)

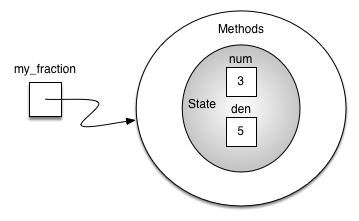
Abstraction and Encapsulation

Since we are using classes to create abstract data types, we should probably discuss the meaning of the word "abstract" in this context. Abstraction in object-oriented programming requires you to focus only on the desired properties and behaviors of the objects and discard what is unimportant or irrelevant.

It is used in a situation where software programmers want to develop similar objects without having to redefine the most similar properties.

The object-oriented principle of encapsulation is the notion that we should hide the contents of a class, except what is absolutely necessary to expose. Hence, we will restrict the access to our class as much as we can, so that a user can change the class properties and behaviors only from methods provided by the class.

Python does not have private data. Instead, you use naming conventions to design classes that encourage correct use. By convention, Python programmers know that any attribute name beginning with an underscore (_) is for a class’s internal use only. Code should use the class’s methods to interact with each object’s internal-use data attributes.

Attributes whose identifiers do not begin with an underscore (_) are considered publicly accessible.

class Fraction:
    """Class Fraction"""
    def __init__(self, top, bottom):
        """Constructor definition"""
        self._num = top
        self._den = bottom

Polymorphism

Polymorphism means the ability to appear in many forms. In OOP, polymorphism refers to the ability to process objects or methods differently depending on their data type, class, number of arguments, etc. For example, we can overload a constructor with different numbers and types of arguments to give us more optional ways to instantiate an object of the class in question.

In this case, we can use class methods which are associated with a class rather than individual objects like regular methods are. You can recognize a class method in code when you see two markers: the @classmethod decorator before the method’s def statement and the use of cls as the first parameter.

We can then provide alternative constructor methods besides __init__() to implement polymorphism. Here, we can add additional constructors to handle fractions that are whole numbers and instances with no parameters given:

class Fraction:
    """Class Fraction"""
    def __init__(self, top, bottom):
        """Constructor definition"""
        self._num = top
        self._den = bottom
    @classmethod
    def fromTop(cls, top):
        return Fraction(top, 1)
    @classmethod
    def fromVoid(cls):
        return Fraction(0, 1)

The cls parameter acts like self except self refers to an object, but the cls parameter refers to an object’s class. This means that the code in a class method cannot access an individual object’s attributes or call an object’s regular methods. Class methods can only call other class methods or access class attributes.

Calling the constructor with two arguments will invoke the first method, calling it with a single argument will invoke the second method, and calling it with no arguments will invoke the third method.

Using optional parameters will accomplish the same task in this case. Since the class will behave the same no matter which implementation you use and the user will have no idea which implementation was chosen, this is an example of encapsulation.

class Fraction:
    """Class Fraction"""
    def __init__(self, top=0, bottom=1):
        """Constructor definition"""
        self._num = top
        self._den = bottom

Operator overloading

The next thing we need to do is implement the behavior that the abstract data type requires. To begin, consider what happens when we try to print a Fraction object.

my_fraction = Fraction(3, 5)
print(my_fraction)

<__main__.Fraction object at 0x00000285AA5D3C40>

The print function requires that the object convert itself into a string so that the string can be written to the output. This is not what we want. In Python, all classes have a set of standard methods that are provided but may not work properly. One of these, __str__, is the method to convert an object into a string.

What we need to do is provide a better implementation for this method. We will say that this implementation overrides the previous one, or that it redefines the method’s behavior.

class Fraction:
    """Class Fraction"""
    def __init__(self, top, bottom):
        """Constructor definition"""
        self._num = top
        self._den = bottom
    def __str__(self):
        return f"{self._num}/{self._den}"
    
my_fraction = Fraction(3, 5)
print(my_fraction)
print(f"I ate {my_fraction} of pizza")
str(my_fraction)

3/5
I ate 3/5 of pizza

'3/5'

We can override many other methods for our new Fraction class. Some of the most important of these are the basic arithmetic operations.

f1 = Fraction(1, 4)
f2 = Fraction(1, 2)
f1 + f2

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
~\AppData\Local\Temp\ipykernel_19312\3976513727.py in <module>
      1 f1 = Fraction(1, 4)
      2 f2 = Fraction(1, 2)
----> 3 f1 + f2

TypeError: unsupported operand type(s) for +: 'Fraction' and 'Fraction'

We can fix this by providing the Fraction class with a method that overrides the addition method. In Python, this method is called __add__ and it requires two parameters. The first, self, is always needed, and the second represents the other operand in the expression.

def gcd(m, n):
    while m % n != 0:
        m, n = n, m % n
    return n

class Fraction:
    """Class Fraction"""
    def __init__(self, top, bottom):
        """Constructor definition"""
        self._num = top
        self._den = bottom
    def __str__(self):
        return f"{self._num}/{self._den}"
    def __add__(self, other_fraction):
        new_num = self._num * other_fraction._den + \
                     self._den * other_fraction._num
        new_den = self._den * other_fraction._den
        common = gcd(new_num, new_den)
        return Fraction(new_num // common, new_den // common)
    
f1 = Fraction(1, 4)
f2 = Fraction(1, 2)
print(f1 + f2)

3/4

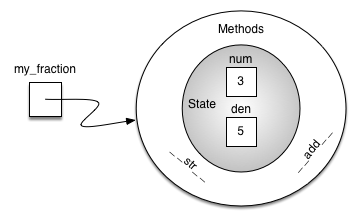
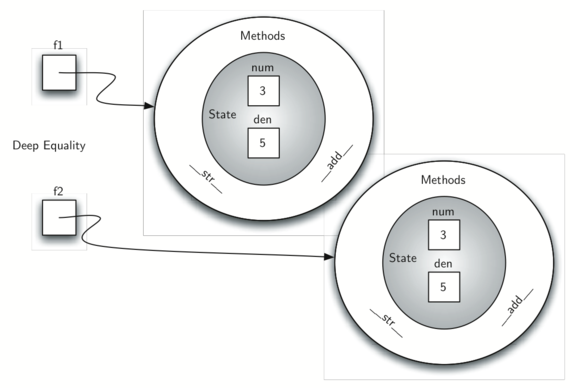
An additional group of methods that we need to include in our example Fraction class will allow two fractions to compare themselves to one another. Assume we have two Fraction objects, f1 and f2. f1==f2 will only be True if they are references to the same object.

Two different objects with the same numerators and denominators would not be equal under this implementation. This is called shallow equality

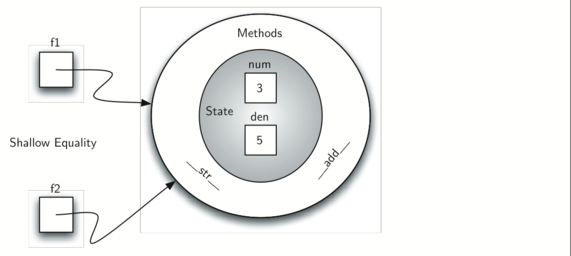
We can create deep equality–equality by the same value, not the same reference–by overriding the __eq__ method

def gcd(m, n):
    while m % n != 0:
        m, n = n, m % n
    return n

class Fraction:
    def __init__(self, top, bottom):
        self._num = top
        self._den = bottom

    def __str__(self):
        return "{:d}/{:d}".format(self._num, self._den)

    def __eq__(self, other_fraction):
        first_num = self._num * other_fraction._den
        second_num = other_fraction._num * self._den

        return first_num == second_num

    def __add__(self, other_fraction):
        new_num = self._num * other_fraction._den \
        + self._den * other_fraction._num
        new_den = self._den * other_fraction._den
        cmmn = gcd(new_num, new_den)
        return Fraction(new_num // cmmn, new_den // cmmn)

x = Fraction(1, 2)
y = Fraction(2, 3)
print(y)
print(x + y)
print(x == y)

2/3
7/6
False

Exercise: Implement the remaining relational operators __gt__, __lt__. In the definition of fractions we assumed that negative fractions have a negative numerator and a positive denominator. Using a negative denominator would cause some of the relational operators to give incorrect results. In general, this is an unnecessary constraint. Modify the constructor to allow the user to pass a negative denominator so that all of the operators continue to work properly.

## Your code here

1.13.2. Inheritance: Logic Gates and Circuits

Inheritance is the ability of one class to be related to another class. Children inherit characteristics from their parents. Similarly, Python child classes can inherit characteristic data and behavior from a parent class. These classes are often referred to as subclasses and superclasses.

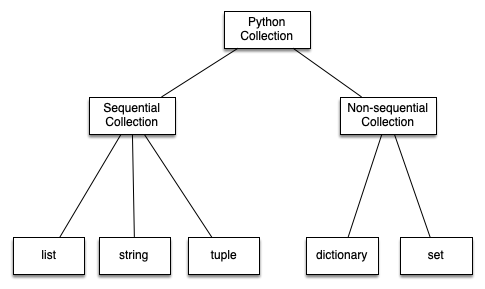
For example, the list is a child of the sequential collection. In this case, we call the list the child and the sequence the parent (or subclass list and superclass sequence). This is often referred to as an Is-a relationship (the list Is-a sequential collection).

Lists, tuples, and strings are all examples of sequential collections. They all inherit common data organization and operations. However, each of them is distinct based on whether the data is homogeneous and whether the collection is immutable. The children all gain from their parents but distinguish themselves by adding additional characteristics.

By organizing classes in this hierarchical fashion, object-oriented programming languages allow previously written code to be extended to meet the needs of a new situation.

To explore this idea further, we will construct a simulation, an application to simulate digital circuits. The basic building block for this simulation will be the logic gate. These electronic switches represent Boolean algebra relationships between their input and their output.

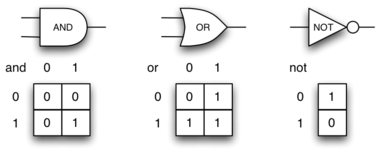
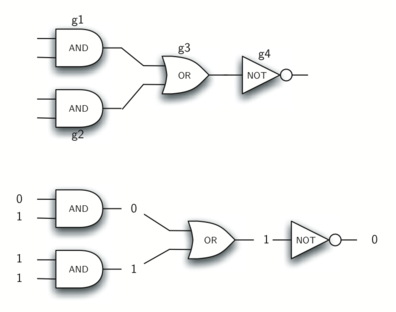
In order to implement a circuit, we will first build a representation for logic gates. Logic gates are easily organized into a class inheritance hierarchy:

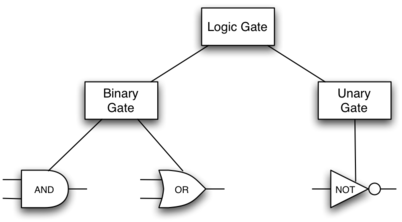
We can now start to implement the classes by starting with the most general, LogicGate. As noted earlier, each gate has a label for identification and a single output line. In addition, we need methods to allow a user of a gate to ask the gate for its label.

class LogicGate:
    def __init__(self, lbl):
        self._label = lbl
        self._output = None

    def get_label(self):
        return self._label

    def get_output(self):
        self._output = self.perform_gate_logic()
        return self._output

At this point, we will not implement the perform_gate_logic(). The reason for this is that we do not know how each gate will perform its own logic operation. Those details will be included by each individual gate that is added to the hierarchy.

Any new logic gate that gets added to the hierarchy will simply need to implement the perform_gate_logic() and it will be used at the appropriate time. Once done, the gate can provide its output value.

class BinaryGate(LogicGate):
    def __init__(self, lbl):
        LogicGate.__init__(self, lbl) # super().__init__(lbl)
        self._pin_a = None
        self._pin_b = None

    def get_pin_a(self):
        if self._pin_a == None:
            return int(input("Enter pin A input for gate " + self.get_label() + ": "))
        else:
            return self._pin_a.get_from().get_output()
    def get_pin_b(self):
        if self._pin_b == None:
            return int(input("Enter pin B input for gate " + self.get_label() + ": "))
        else:
            return self._pin_b.get_from().get_output()
        
    def set_from_pin(self, source):
        if self._pin_a == None:
            self._pin_a = source
        else:
            if self._pin_b == None:
                self._pin_b = source
            else:
                raise RuntimeError("Error: NO EMPTY PINS")

The call to set_from_pin() is very important for making connections.

class UnaryGate(LogicGate):

    def __init__(self, lbl):
        LogicGate.__init__(self, lbl)

        self._pin = None

    def get_pin(self):
        if self._pin == None:
            return int(input("Enter pin input for gate " + self.get_label() + ": "))
        else:
            return self._pin.get_from().get_output()

    def set_from_pin(self, source):
        if self._pin == None:
            self._pin = source
        else:
            print("Cannot Connect: NO EMPTY PINS on this gate")

The constructors in both of these classes start with an explicit call to the constructor of the parent class using the parent’s __init__ method. The constructor then goes on to add the two input lines (pin_a and pin_b).

Now that we have a general class for gates depending on the number of input lines, we can build specific gates that have unique behavior. For example, the AndGate class will be a subclass of BinaryGate since AND gates have two input lines

class AndGate(BinaryGate):
    def __init__(self, lbl):
        super().__init__(lbl)

    def perform_gate_logic(self):
        a = self.get_pin_a()
        b = self.get_pin_b()
        if a == 1 and b == 1:
            return 1
        else:
            return 0

g1 = AndGate("G1")
g1.get_output()

Enter pin A input for gate G1: 0
Enter pin B input for gate G1: 1

0

The same development can be done for OR gates and NOT gates:

class OrGate(BinaryGate):

    def __init__(self, lbl):
        BinaryGate.__init__(self, lbl)

    def perform_gate_logic(self):

        a = self.get_pin_a()
        b = self.get_pin_b()
        if a == 1 or b == 1:
            return 1
        else:
            return 0

class NotGate(UnaryGate):

    def __init__(self, lbl):
        UnaryGate.__init__(self, lbl)

    def perform_gate_logic(self):
        if self.get_pin():
            return 0
        else:
            return 1

g2 = OrGate("G2")
print(g2.get_output())

g3 = NotGate("G3")
g3.get_output()

Enter pin A input for gate G2: 1
Enter pin B input for gate G2: 0
1
Enter pin input for gate G3: 1

0

Now that we have the basic gates working, we can turn our attention to building circuits. In order to create a circuit, we need to connect gates together, the output of one flowing into the input of another. To do this, we will implement a new class called Connector.

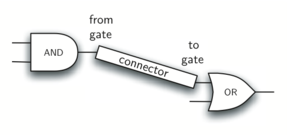
The Connector class will not reside in the gate hierarchy. It will, however, use the gate hierarchy in that each connector will have two gates, one on either end. This relationship is very important in object-oriented programming. It is called the Has-a relationship.

Now, with the Connector class, we say that a Connector Has-a LogicGate, meaning that connectors will have instances of the LogicGate class within them but are not part of the hierarchy.

class Connector:
    def __init__(self, fgate, tgate):
        self.from_gate = fgate
        self.to_gate = tgate

        tgate.set_from_pin(self)

    def get_from(self):
        return self.from_gate

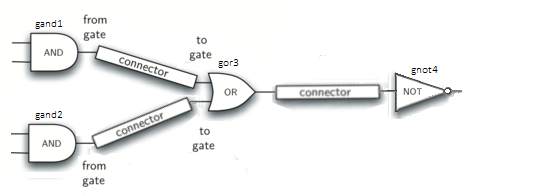
g1 = AndGate("gand1")
g2 = AndGate("gand2")
g3 = OrGate("gor3")
g4 = NotGate("gnot4")
c1 = Connector(g1, g3)
c2 = Connector(g2, g3)
c3 = Connector(g3, g4)
g4.get_output()

Enter pin A input for gate gand1: 0
Enter pin B input for gate gand1: 1
Enter pin A input for gate gand2: 0
Enter pin B input for gate gand2: 1

1

References

1. Texrbook Ch1